This tutorial can be downloaded link.
Intro tutorial 6: Calculation of Localization Factor¶
In this tutorial, we show how to determine the localization factor \(\mathrm{L_n}\) of each Kohn-Sham state. The localization factor is defined as
and describes the localization of the n-th KS wavefunction in a given volume \(V\) within the supercell volume \(\Omega\). Commonly, the localization factor is used to identify localized defect orbitals. More details can be found in N. Sheng, C. Vorwerk, M. Govoni, and G. Galli, J. Chem. Theory Comput. 18, 6, 3512 (2022).
In this tutorial, we will use the localization factor to identify defect orbitals of the \(\mathrm{NV^-}\) center in diamond.
Step 1: Mean-Field Starting Point¶
As a first step, we perform the mean-field electronic structure calculation within density-functional theory (DFT) using the Quantum ESPRESSO code.
Download the following files in your working directory:
[1]:
%%bash
wget -N -q http://www.west-code.org/doc/training/nv_diamond_63/pw.in
wget -N -q http://www.quantum-simulation.org/potentials/sg15_oncv/upf/C_ONCV_PBE-1.0.upf
wget -N -q http://www.quantum-simulation.org/potentials/sg15_oncv/upf/N_ONCV_PBE-1.0.upf
We can now inspect the pw.in file, the input for the pw.x code:
[2]:
%%bash
cat pw.in
&CONTROL
calculation = 'scf'
wf_collect = .true.
pseudo_dir = './'
/
&SYSTEM
input_dft = 'PBE'
ibrav = 0
ecutwfc = 50
nosym = .true.
tot_charge = -1
nspin = 1
nbnd = 176
occupations = 'from_input'
nat = 63
ntyp = 2
/
&ELECTRONS
conv_thr = 1D-08
/
K_POINTS gamma
CELL_PARAMETERS angstrom
7.136012 0.000000 0.000000
0.000000 7.136012 0.000000
0.000000 0.000000 7.136012
ATOMIC_SPECIES
C 12.01099968 C_ONCV_PBE-1.0.upf
N 14.00699997 N_ONCV_PBE-1.0.upf
ATOMIC_POSITIONS crystal
C 0.99996000 0.99996000 0.99996000
C 0.12495000 0.12495000 0.12495000
C 0.99905000 0.25039000 0.25039000
C 0.12350000 0.37499000 0.37499000
C 0.25039000 0.99905000 0.25039000
C 0.37499000 0.12350000 0.37499000
C 0.25039000 0.25039000 0.99905000
C 0.37499000 0.37499000 0.12350000
C 0.00146000 0.00146000 0.50100000
C 0.12510000 0.12510000 0.62503000
C 0.00102000 0.24944000 0.74960000
C 0.12614000 0.37542000 0.87402000
C 0.24944000 0.00102000 0.74960000
C 0.37542000 0.12614000 0.87402000
C 0.24839000 0.24839000 0.49966000
C 0.37509000 0.37509000 0.61906000
C 0.00146000 0.50100000 0.00146000
C 0.12510000 0.62503000 0.12510000
C 0.00102000 0.74960000 0.24944000
C 0.12614000 0.87402000 0.37542000
C 0.24839000 0.49966000 0.24839000
C 0.37509000 0.61906000 0.37509000
C 0.24944000 0.74960000 0.00102000
C 0.37542000 0.87402000 0.12614000
C 0.99883000 0.50076000 0.50076000
C 0.12502000 0.62512000 0.62512000
C 0.99961000 0.74983000 0.74983000
C 0.12491000 0.87493000 0.87493000
C 0.25216000 0.50142000 0.74767000
C 0.37740000 0.62659000 0.87314000
C 0.25216000 0.74767000 0.50142000
C 0.37740000 0.87314000 0.62659000
C 0.50100000 0.00146000 0.00146000
C 0.62503000 0.12510000 0.12510000
C 0.49966000 0.24839000 0.24839000
C 0.61906000 0.37509000 0.37509000
C 0.74960000 0.00102000 0.24944000
C 0.87402000 0.12614000 0.37542000
C 0.74960000 0.24944000 0.00102000
C 0.87402000 0.37542000 0.12614000
C 0.50076000 0.99883000 0.50076000
C 0.62512000 0.12502000 0.62512000
C 0.50142000 0.25216000 0.74767000
C 0.62659000 0.37740000 0.87314000
C 0.74983000 0.99961000 0.74983000
C 0.87493000 0.12491000 0.87493000
C 0.74767000 0.25216000 0.50142000
C 0.87314000 0.37740000 0.62659000
C 0.50076000 0.50076000 0.99883000
C 0.62512000 0.62512000 0.12502000
C 0.50142000 0.74767000 0.25216000
C 0.62659000 0.87314000 0.37740000
C 0.74767000 0.50142000 0.25216000
C 0.87314000 0.62659000 0.37740000
C 0.74983000 0.74983000 0.99961000
C 0.87493000 0.87493000 0.12491000
N 0.48731000 0.48731000 0.48731000
C 0.49191000 0.76093000 0.76093000
C 0.62368000 0.87476000 0.87476000
C 0.76093000 0.49191000 0.76093000
C 0.87476000 0.62368000 0.87476000
C 0.76093000 0.76093000 0.49191000
C 0.87476000 0.87476000 0.62368000
OCCUPATIONS
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00 2.00
2.00 2.00 2.00 2.00 2.00 2.00 1.00 1.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
We can now run pw.x on 2 cores.
[ ]:
%%bash
mpirun -n 2 pw.x -i pw.in > pw.out
We have carried out a spin unpolarized calculation (i.e., nspin = 1) because we want to use \(L_n\) to define an active space for quantum defect embedding theory (QDET, see Tutorial 5). The latter uses a spin-unpolarized mean-field starting point to reduce spin contamination in the generation of the parameters for the effective Hamiltonian.
Step 2: Calculation of the Localization Factor¶
Localization factors are calculated with the westpp.x executable within WEST. You can download the input file with the following command:
[3]:
%%bash
wget -N -q http://www.west-code.org/doc/training/nv_diamond_63/westpp.in
Let us inspect the input file.
[4]:
%%bash
cat westpp.in
wstat_control:
wstat_calculation: S
n_pdep_eigen: 512
westpp_control:
westpp_calculation: L
westpp_range: [1, 176]
westpp_box: [6.19, 10.19, 6.28, 10.28, 6.28, 10.28]
The keyword westpp_calculation: L triggers the calculation of the localization factor. With westpp_range, we can select for which Kohn-Sham states we compute the localization factor. In this tutorial, we use all 176 states. Finally, westpp_box specifies the parameter of a box in atomic units to use for the integration. In this case, we have chosen a cubic box around the carbon vacancy at \(\left( 8.18, 8.28, 8.28 \right)\) Bohr with an edge of 4 Bohr. The box has a volume of 64
Bohr\(^3\), which is smaller than the supercell volume of 2452.24 Bohr\(^3\).
[ ]:
%%bash
mpirun -n 2 westpp.x -i westpp.in > westpp.out
westpp.x creates a file named west.westpp.save/localization.json. If the reader does NOT have the computational resources to run the calculation, the WEST output file needed for the next step can be directly downloaded as:
[5]:
%%bash
mkdir -p west.westpp.save
wget -N -q http://www.west-code.org/doc/training/nv_diamond_63/localization.json -O west.westpp.save/localization.json
We can now visualize the results:
[6]:
import json
import numpy as np
import matplotlib.pyplot as plt
with open('west.westpp.save/localization.json', 'r') as f:
data = json.load(f)
y = np.array(data['localization'],dtype='f8')
x = np.array([i+1 for i in range(y.shape[0])])
plt.plot(x,y,'o')
plt.xlabel(r'$\mathrm{KS \; Index}$')
plt.ylabel(r'$\mathrm{Localization \; Factor}$')
plt.show()
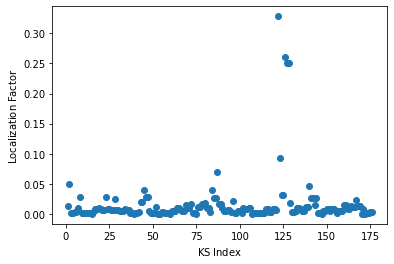
We see that a number of Kohn-Sham orbitals have a high localization factor.
[7]:
print(x[y>=0.08])
[122 123 126 127 128]
The highest localization factor (>0.08) is found for the Kohn-Sham orbitals with the index 122, 123, 126, 127, and 128.